2021. 6. 7. 11:09ㆍ베이지안 딥러닝
Bell shape에 x축 : x-x'이라는 거리.
거리가 가까워지면 k가 커짐. 거리가 멀어지면 k가 작아짐.
kernel function의 의미 : 입력과 바로 옆 입력이 얼마가 비슷한지.
Kernel function이 존재하면 이걸로 span된 공간이 정의됨. 이 공간 : RKHS.
- GPLVM은 non-linear probabilistic PCA (PPCA) 이라고 한다.
- Dimension reduction
- Non-linear mapping
이번시간 : PPCA와 GPLVM의 관계에 대해서 살펴보자.
PCA = SVD
Singular value : 축이 얼마나 중요한지.
$$W^{T}:\mathbb{R}^{n\times q}\rightarrow\mathbb{R}^{n\times q}$$
by $Y=XW^{T}$ where $W\in\mathbb{R}^{d\times q}$.
$$Y\overset{W}{\rightarrow}X\overset{W^{T}}{\rightarrow}Y$$
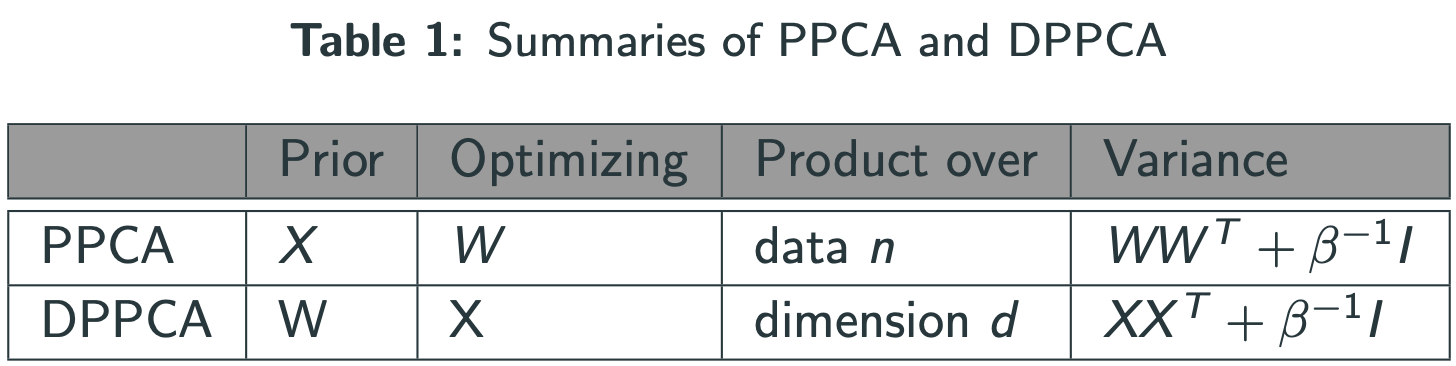
1) $W^{T}$ 에 대해서 보자. (Probabilistic PCA)
- 가정 1
- $X$ 를 iid, Gaussian이라고 가정
- 가정 2
- $$p(Y|X,W)=\Pi_{i=1}^{n}\mathcal{N}(y_{(i)}|Wx_{(i)},\beta^{-1}I)$$
Marginal likelihood
$$p(Y|W)=\int_{X}p(Y|X,W)p(X)dX$$
likelihood구한 이유 : 얘를 maximize하는 W를 찾자.
log취하고, 미분=0 => Solution : $$\hat{W}=U_{q}LV^{T}$$
where $U_{q}$ and $Λ_{q}$ are first $q$ eigenvectors and eigenvalues of $Y^{T}Y$ , $L = (Λ_{q} − β^{−1} I)^{1/2}$ , and $V$ is an arbitrary rotation matrix.
Note : $Λ_{q}$의 diagonal term은 모두 양수(symmetric, p.s.d)
$\beta^{-1}$ 이 $Λ_{q}$를 줄여주는 역할. SVD로 축을 만들면, 그 축을 얼마나 믿을지에 대한 정보를 $\beta^{-1}$ 로 잡음.
measurement noise에 해당하는 term = $\beta^{-1}$
2) $W$ 에 대해서 보자.(Dual Probabilistic PCA)
- 가정 1
- $W$ 를 iid, Gaussian이라고 가정
- 가정 2
- $$p(Y|X,W)=\Pi_{i=1}^{n}\mathcal{N}(y_{(i)}|Wx_{(i)},\beta^{-1}I)$$
Marginal likelihood
$$p(Y|X)=\int_{W}p(Y|X,W)p(W)dW$$
log취하고, 미분=0 => Solution : $$\hat{X}=U_{q}LV^{T}$$
where $U_{q}$ and $Λ_{q}$ are first $q$ eigenvectors and eigenvalues of $YY^{T}$ , $L = (Λ_{q} − β^{−1} I)^{1/2}$ , and $V$ is an arbitrary rotation matrix.
Note : $YY^{T}$ 가 kernel matrix -> Dual Probabilistic PCA = Kernel PCA
Gaussian Process Latent Variable(GPLVM)
- Gaussian process prior의 의미
- Y는 X가 비슷하면 smooth해짐.
- X : latent space , Y : observed data(image)에서 이미지가 조금 변하면 latent space에서도 조금 변하게 만들고 싶음.
- t-sne
- observed space에서 거리상의 비율이 latent space에서 거리상의 비율가 비슷하게 만들어줌.
- 이런 가정들이 있는 learning = Manifold learning이라고 부름
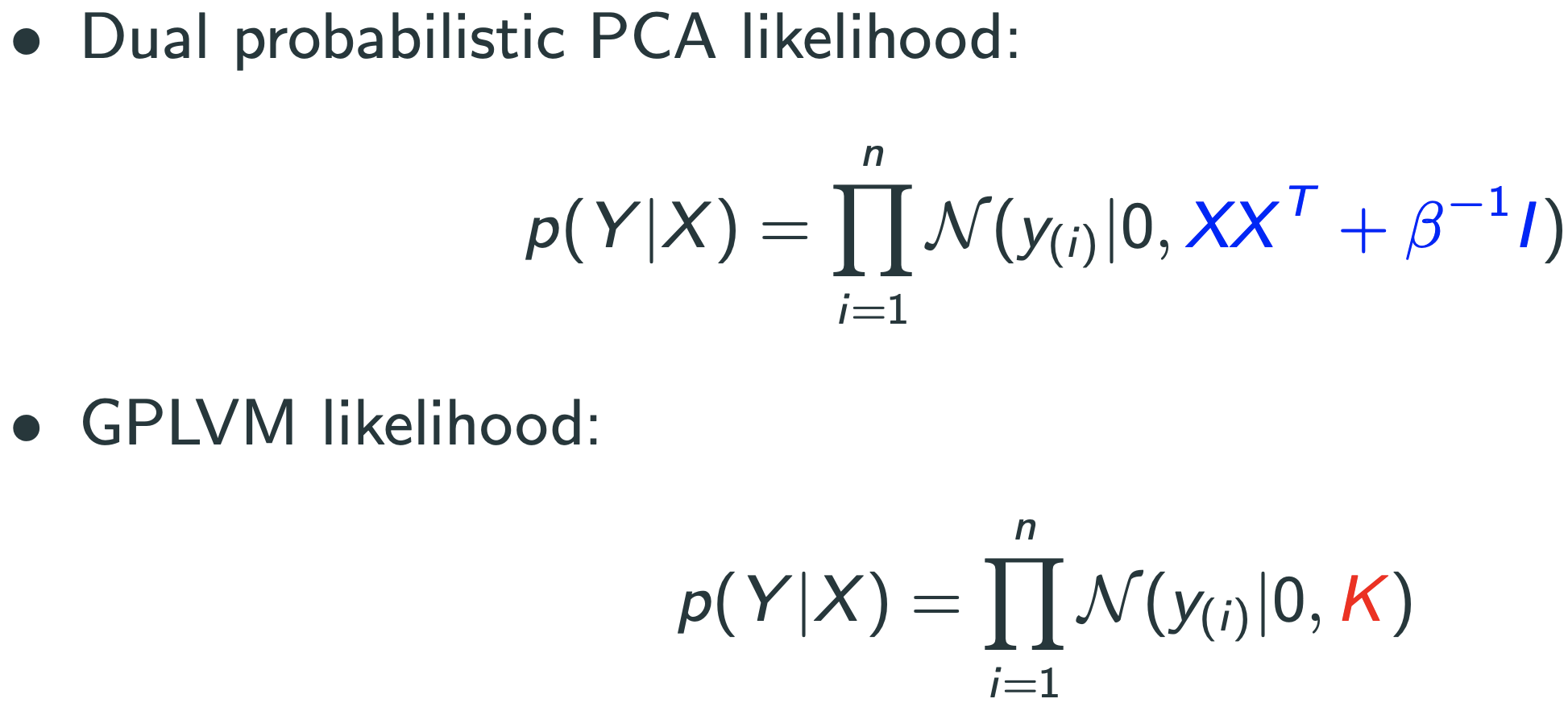
Note : X의 초기값은 Y의 PCA로 주기도 함.
GPLVM의 단점 : 역시 K의 inverse를 구해야 하므로 $O(n^{3})$. 따라서 데이터가 많으면 쓰기 힘듦.
'베이지안 딥러닝' 카테고리의 다른 글
| Gaussian Process의 Weight space view | Function space view (0) | 2021.06.03 |
|---|---|
| Functional analysis (2) | 2021.05.28 |
| Random process (1) | 2021.05.27 |
| Introduction, Set theory, Measure theory, Probability, Random variable (0) | 2021.05.26 |
