Functional analysis

 

Space 정의

inner product를 정의할수 있으면, norm을 정의할 수 있고, norm을 정의할 수 있으면, metric을 정의할 수 있다.

이번 시간 : Inner product, Hilbert space, Kernel, Positive definite, Eigenfunction and eigenvalue, Mercer’s theorem, Bochner’s theorem, Reproducing kernel Hilbert space (RKHS), Moore-Aronszajn theorem, Representer theorem

inner product 정의

위 inner product정의로 norm을 정의할 수 있음

Hilbert space 정의

Kernel 정의

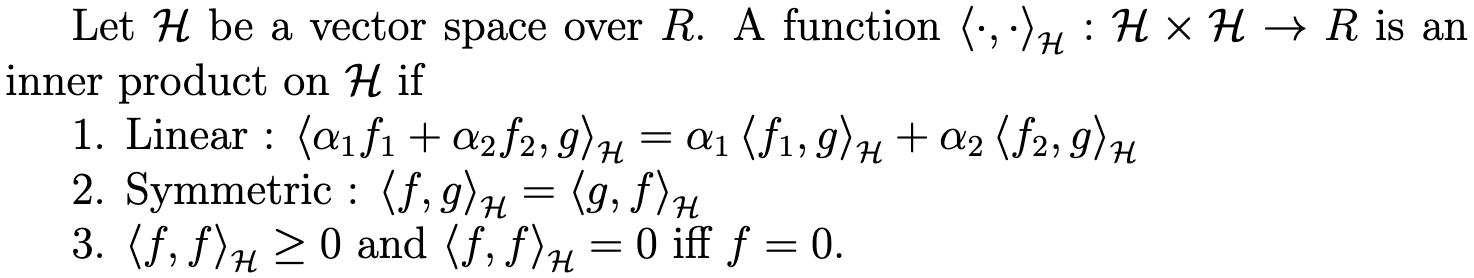
kernel은 set X에 많은 조건이 필요 없다.

Kernel공부하면서 나온 이야기 : 

분류 문제 : binary classification : shatter(ML에서)

입력공간에 빨간색 공, 파란색 공. 나누기.

선 하나로 나눌수 있나?

나눌수 없다면, 차원을 높혀서(2차원,3차원) 선형분류기로 항상 분류할 수 있음.

따라서 kernel function으로 분류하면 항상 선으로 모든것을 분류할 수 있다.: kernel method의 정당성

주의할 점, 맹점 : 가지고 있는 학습 데이터는 잘 분류하지만, 새로운 test 데이터에서는 안될 수 있음.

 

Hilbert space가 아닌건 생각이 안남(Banach space. 1-norm 공간)

Function space에서 Function space로 보내는 operator. Finite 차원에서는 행렬로 생각할 수 있음.

선형대수학 : 일반 함수를 matrix의 map으로 생각할 수 있음

=> 함수 : basis와 coefficient로 나타낼 수 있음.

이때 coefficient를 구하기 위해 필요한 것 : inner product

이 행위를 function에서 해보자! : Hilbert space를 생각해보자!

무한 차원에서 만들어진 함수가 수렴한다는 것을 보이기 위해서 completeness가 필요함.

kernel : positive definite 정의. positive semi-definite아닌가?

 

Kernel의 eigenfunction, eigenvalue

Mercer theorem. 조건에 kernel이 symmetric이어야 함. 한마디로 Kernel이 continuous, spsd(=symmetric positive semi-definite)이면 eigenvalue,eigenfunciton이 존재하고, diagnoalizable하게 표현됨. Absolutely summable해서 finite sum으로 epsilon-근사할 수 있음.

isotropic kernel function : 어떤 kernel function이 두 입력의 거리 함수

$$ k(x, x_0 ) = k_I(t = |x − x_0 |)

$$

 

* Corollary (Bochner) <----다시 보자

Gaussian process의 kernel은 auto correl. function이다. gaussian processe에서 auto-correlation function(acf)를 생각할수 있다. 여기서, covariance matrix는 positive semi-definite이다.

의문점 : random(or gaussian) process의 acf는 항상 positive semi-definite인가?(28분~30분20초) No!

 

RKHS

RKHS 정의

앞으로는 대부분의 공간이 RKHS이다. (RKHS = reproducing kernel Hilbert space)

RKHS이면, H에서 정의된 f가 diagonalizable하다. 이게 SVD의 확장! (두번째 등호에서 Fubini's theorem 사용됨)

Kernel function은 기울기를 정의하는 것과 같다.

함수(kernel function)를 매우 steep 하게 잡으면 그 결과 공간도 steep하게 된다.

함수를 부드럽게 잡으면 그 결과 공간도 부드럽게 된다.

의미 : kernel이 하나 존재하면 그에 해당하는 RKHS space도 존재한다.

kernel이 존재할때 space 찾는 방법 :

함수를 찾는 문제가 dataset의 크기 n에 대해 n개의 $\alpha_i$ 를 찾는 문제로 바뀜.

n개의 dataset에서 fitting하는 함수를 찾는 문제가 n개의 값 찾는 문제로 둔갑.

예제. 풀어보자. 자세히 안봄.

 

의문점

• Mercer theorem과 Spectral theorem은 어떻게 다르지?
  • Mercer theorem은 Kernel에서 정의됨(2개 input). 여기서 eigenvalue, eigenfunction을 말함.
  • Spectral theorem은 compact operator에 정의됨. 여기서 eigenvalue, eigenfunction을 말함.
  • 강의에는 Mercer theorem이 SVD의 infinite dimensional case라고 나오는데, Spectral theorem이 더 맞아보임.
    • 요것도 좀 다름. SVD는 symmetric조건이 필요 없음.
• positive semi-definite이 아닌 kernel도 존재하나?
  • YES!
• Covariance matrix가 positive semi-definite이 아닐수 있나?
  • No. 항상 p.s.d 증명