Gaussian Process
2021. 6. 1. 15:02ㆍ카테고리 없음
pdf download
Gaussian Process의 정의 :
a collection of random variables, any finite number of which have a joint Gaussian distribution.
한글 : random variables의 모음. 유한개의 variables가 joint Gaussian이 되는.
- 1개 :
- univariate Gaussian distribution
- 여러개 :
- multivariate Gaussian distribution
- central limit theorem
- Conditional probability도 gaussian이다.(mean, var의 모양은 복잡함)
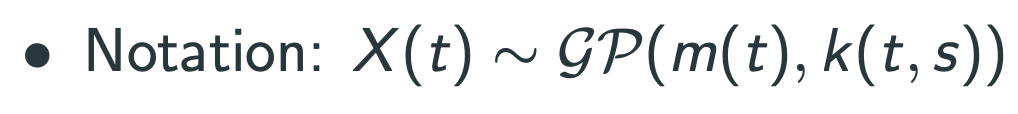
where $$k(t,s) = Cov(X(t),X(s))$$.
이 Kernel function은 반드시 p.s.d여야 한다!(이유는 뒤 강의에서 살펴볼 예정)
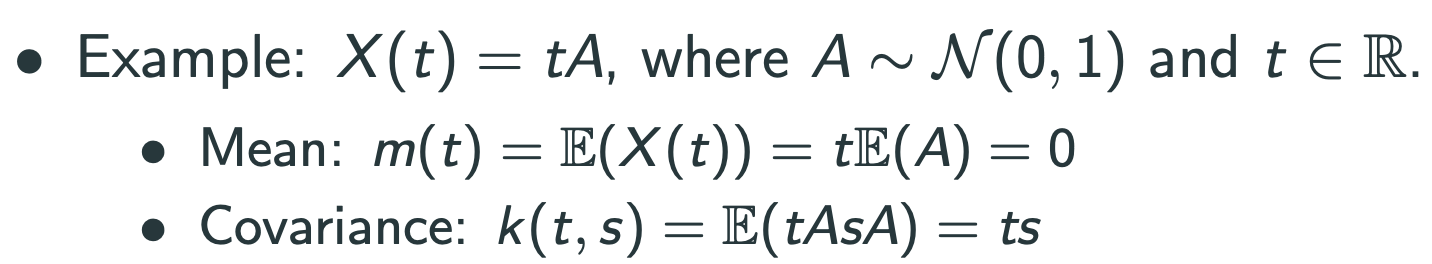
GPR
GP와 GPR은 다르다
- GPR = Gaussian process regression :
- A nonparametric Bayesian regression method using the properties of Gaussian processes
- GP의 좋은 성질들을 이용해서 regression을 하는 것.
7분 30초에 빠르게 넘어가지만, 무슨 말인지 모르겠음.
- GPR의 두가지 view
- Weight-space view
- Function-space view
- 결국 두개가 동치임을 보일 예정.
의문점:
- k(t,s) = ts 행렬은 p.s.d가 되나?
- Yes! 증명: 먼저 rank가 1이다. 그리고 symmetric하다. 따라서 n개 eigenvalue존재.
- 모든 eigenvalue sum = trace >0 따라서 eigenvalues : a,0,0,...,0이고, a는 양수.
- Yes! 증명: 먼저 rank가 1이다. 그리고 symmetric하다. 따라서 n개 eigenvalue존재.
